Averages Aptitude Questions and Answers | MCQ Problems: Ready to Take Averages Aptitude Test? Well, through this Quiz you can easily Work on the Averages Topics. This will help you in clearing the topics easily. And we are going to help you with that. And here on this page, we are providing the Averages Formulae along with some Shortcuts and Tricks. Well, we hope that all these will help you to become a pro in that topic. Therefore, check them. And then proceed to take the Averages Quiz Online Test. Now, the Test will be in the Objective Form. That means you are going to attempt the Averages MCQ Problems Quiz Online Test below. So, after attempting each question, you can easily check the answer. This will also reduce your search time for the Answers in another place. Along with the Answers we are also providing Quick solutions and Explanations too. Therefore, work on that. Check further.
Averages Aptitude Questions and Answers | Averages MCQ Problems
| Quiz Name | Averages |
| Category | Aptitude |
| Number of Questions | 25 |
| Time | 30 Minutes |
| Exam Type | MCQ (Multiple Choice Questions) |
Averages Aptitude Quiz – Practice Now
★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★
1. 20 boys go for dinner. 16 of them spent Rs. 64 each on their dinner and rest spent Rs 4 more than the average expenditure of all 20. What was the total money spent by them?
a. 1200
b. 1500
c. 1800
d. 1300
e. None of these
Answer: d
Explanation:
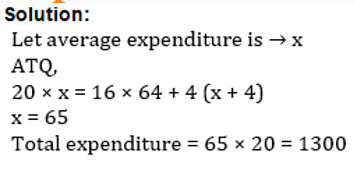
2. The average of 6 consecutive even numbers is 13. What is the product of the greatest and lowest numbers among them?
a. 144
b. 162
c. 126
d. 90
e. 108
Answer: a
Explanation:
Let the 6 consecutive even numbers be, (a, a+2, a+4, a+6, a+8, a+10)
As, average = 13
So, the sum of 6 consecutive even numbers = 13*6 =78
So, a+ a+2 + a+4 + a+6 + a+8 + a+ 10 = 78
6a + 30 = 78
6a = 78 – 30 = 48
So, a = 48/6 = 8
So, the largest even numbers in these numbers = a+ 10 = 18
And lowest number = a = 8
So, required product = 18* 8 =144
3. The average weight of a group of 50 boys is 60 kg. When 5 boys whose average weight is 80 kg left the group and 10 boys whose average weight is 70 kg joined the group, then find the new average weight of the group?
a. 64 kg
b. 65 kg
c. 60 kg
d. 62 kg
e. 70 kg
Answer: c
Explanation:
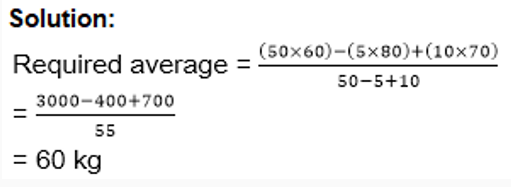
4. Average expenditure of Manoj & Nawaz is Rs 4500 which is 10% less than that of Sanjay & Irfan. If Sanjay spends Rs 500 more than Nawaz & average expenditure of Nawaz & Sanjay is Rs 4250. Find average expenditure of Manoj & Irfan. (in Rs)
a. 4250
b. 5000
c. 4750
d. 5250
e. 4500
Answer: d
Explanation:
let Sanjay spends Rs x.
Expenditure of Nawaz = x – 500 Rs
ATQ, x+x-500=8500
X= Rs 4500
5. The average of four consecutive odd numbers A, B, C and D respectively is 24. What is the product of B and D?
a. 384
b. 475
c. 621
d. 625
e. None of these
Answer: c
Explanation:
Let the odd number A, B, C and D be x, (x + 2), (x + 4) and (x + 6) respectively.
Now, according to the question,
x + (x + 2) + (x + 4) + (x + 6) = 4 × 24
⇒ 4x + 12 = 96
⇒ 4x = 84
⇒ x = 21
So, B = 21 + 2 = 23 and D = x + 6 = 21 + 6 = 27
Required answer = B × D = 23 × 27 = 621
6. The average marks obtained by 80 students in Math is 42. If the average marks of the passed students is 48 while the average marks of the failed students is 32, then find the difference of number of students who passed and failed in the math exam.
a. 30
b. 40
c. 50
d. 60
e. 20
Answer: e
Explanation:
Let passed students and failed students be P and F
42 × 80 = 48 × P + 32 × F ……(i)
and P + F = 80 …….(ii)
By solving (i) and (ii) , we get
P = 50 and F =30
Required difference = 50 – 30 = 20
7. There are two sections in a company. Section A has 30 employees and section B has 40 employees. The average salary of employees of section A and employees of section B is Rs. 5000 and Rs. 6000 respectively. Find the average salary of all the employees in the company.
a. Rs. 5571.43
b. Rs. 5000.02
c. Rs. 4872.12
d. Rs. 5000
e. None of these
Answer: a
Explanation:
The required average salary of all the employees in the company
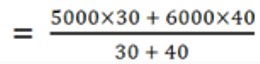
= Rs. 5571.428
8. Rohit Sharma has a certain average of runs for 14 innings. In a match against Australia, he played his 15th inning in which he was awarded man of the match for scoring 72 runs, thereby increasing his average by 2 runs. Find his average after playing with Australia.
a. 42
b. 44
c. 46
d. 40
e. None of these
Answer: b
Explanation:
Let the average till 14 thinnings be x.
Average after 15thinnings = (X + 2)
Then, 14x + 72 = 15(x + 2)
⇒ X = 42.
Hence average after 15 thinning will be x + 2 = 42 + 2 = 44
9. The average age of 70 workers in a factory is 42. The average age of the men is 50 and that of the women is 30. What is the number of women working in the factory?
a. 18
b. 16
c. 25
d. 40
e. 28
Answer: e
Explanation:
Let the number of women working in the factory be x.
Number of men working in the factory = (70 – x)
10. The average score of A, B and C is 63. A’s score is 15 less than D and 10 more than B’s score. If D scored 30 marks more than the average score of A, B and C, then what is the sum of B’s and C’s scores?
a. 120
b. 111
c. 117
d. Cannot be determined
e. None of these
Answer: b
Explanation:
Let score of B = x
Score of A = x + 10
Score of D = x + 25 = 63 + 30
⇒ x = 68
Score of A = 68 + 10 = 78
Total score of A, B and C = 189
Required Sum (B + C)’s score = 189 – 78 = 111
11. Average of 11 numbers is 71 and the average of first 5 numbers is 73. If average of last 4 numbers is 84 and the ratio of 6th and 7th number is 9 : 7, then find the 6th number.
a. 27
b. 36
c. 45
d. 54
e. None of these
Answer: c
Explanation:
Let the 6th number = 9x, then 7th number = 7x
According to question
11 × 71 = 5 × 73 + 9x + 7x + 4 × 84
⇒ 781 = 365 + 16x + 336
⇒ 16x = 781 – (365 + 336) = 80
⇒ x = 80/16 = 5
Hence, the 6th number = 9x = 9 × 5 = 45
12. The average weight of 16 employees in a company is 63 kg. The average weight of the first 5 employees is 58 kg and the average weight of the next 9 employees is 62 kg. If the weight of 15th employee is 12 kg more than 16th employee, find the weight of the 15th employee.
a. 76 kg
b. 72 kg
c. 86 kg
d. 78 kg
e. 60 kg
Answer: c
Explanation:
Sum of weight of 15th and 16th employees = 16 × 63 – 5 × 58 – 9 × 62 = 160 kg
Let the weight of 16th employee be x kg.
Then, (x + 12) + x = 160
⇒ x = 74
Weight of 15th employee = 74 + 12 = 86 kg
Hence, option C is correct.
13. In a class of 50 students, 42 students scored an average of 95 marks out of 100 in English. The remaining 8 students have scores differing by 1 mark each. If the average of the class is 92.6, find the marks of the student who stood second highest among the remaining 8 students.
a. 83.2
b. 84.4
c. 82.5
d. 81.8
e. 86.5
Answer: c
Explanation:
Total marks of 42 students = 42 × 95 = 3990
Total marks of class = 50 × 92.6 = 4630
Marks of remaining 8 students = 4630 – 3990 = 640
Let the marks of the student who scores second highest be x.
Using the data from the question, we get
(x + 1) + x + (x – 1) + … + (x – 6) = 640
⇒ 8x – 20 = 640
⇒ 8x = 660
⇒ x = 82.5
Hence, option C is correct
14. Of three numbers, the first is twice the second and the second is twice the third. The average of the reciprocal of the numbers is 7/72 . The numbers are:
a. 16, 8, 4
b. 20, 10, 5
c. 24, 12, 6
d. 36, 18, 9
e. Can’t be determined
Answer: c
Explanation:
15. The average of 19 results is 122. If the average of first 10 results is 92 and that of the last 10 results is 149, then what will be the 10 result?
a. 0
b. 92
c. 82
d. 111
e. None
Answer: b
Explanation:
Here, Total marks = 19 × 122 = 2318
Marks of First 10 results = 10 × 92 = 920
Marks of Last 10 results = 10 × 149 = 1490
So, marks of 10th result = 1490 + 920 − 2318 = 92
16. Among three numbers, the second is thrice the first and also 6 times the third. If the average of the three numbers is 63, then the largest number is:
a. 115
b. 126
c. 96
d. 168
e. None
Answer: b
Explanation:
Let, Third no. = x
Then, Second no. = 6x
And, First no. = 2x
Average of the three numbers = (2x + 6x + x)/3 = 9x/3 = 3x.
Since, 3x = 63
⇒ x = 21.
Thus, Largest number = 6x = 6 × 21 = 126.
17. The average monthly salary of the workers in the workshop is Rs. 9,900. If the average monthly salary of 7 technicians is Rs. 11,200 and average monthly salary of the rest is Rs. 8,600, the total number of workers in the workshop is
a. 17
b. 14
c. 18
d. 11
e. None
Answer: b
Explanation:
18. There are 63 students in a class. Due to the admission of 14 more students, the expenses of the class are increased by Rs 77 per day while the average expenditure per head decreased by Re 1. What was the original expenditure of the class?
a. Rs 693
b. Rs 713
c. Rs 535
d. Rs 854
e. None
Answer: a
Explanation:
Let the original average expenses is Rs x.
∴ According to the question,
77(x-1) – 63x = 77
⇒ 77x-77-63x=77
⇒ 14x= 154 ⇒ x= 11
∴ Original expenditure= 11×63= Rs 693
Hence, option A is the correct answer.
19. The batting average of a cricket player for 64 innings is 62 runs. His highest score exceeds his lowest score by 180 runs. Excluding these two innings, the average of remaining innings becomes 60 runs. What is his highest score?
a. 180 runs
b. 209 runs
c. 212 runs
d. 214 runs
e. None
Answer: d
Explanation:
Let the highest and lowest score be L and H respectively.
We are given that the sum of the highest and the lowest score,
H + L = 64 × 62 – 62 × 60
H + L = 62 × 4 = 248 ………….(i)
Given that,
H – L = 180 …………..(ii)
Adding eq.(i) and (ii):
∴ 2H = 248 + 180
∴ H = 214
Hence, the Highest score = 214
20. The average of 25 number is 56. The average of first 13 numbers is 70 and the average of last 13 numbers is 80. If the 13th number is excluded, then what is the average of the remaining numbers?
a. 30.78
b. 35.42
c. 67.28
d. 28.09
e. None
Answer: b
Explanation:
★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★
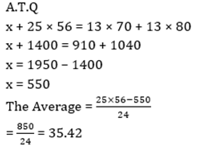
Averages – Formulae
So, in this section, we are going to provide the aspirants who are willing to train themselves in the Averages with the Basic Formulas. While cracking any of the problems, these formulae will come in handy for you all. Therefore, try to check them. And memorize them. Now, apply these fundamentals to some problems. And after feeling confident, try to take the Quiz. Then eventually, you will get a grip on the topic. Well, below, you got two different formula’s. And one is to calculate the Normal Average, while the other is to calculate the Average Speed.
- Average = (Sum of observations / Number of observations)
- Average Speed = (2xy)/ (x+Y) kmph
Averages Quiz Questions
Now, our team from Freshers Now has done brilliant research. And framed the Questions in an understandable, yet tricky manner. So, an individual who is preparing for the different levels of Exams can get the Practise. Now, there is no limit that you have to taking the Test only once. You can proceed and take the Test, as many times as you wish to do so. Amazing right?
Practice More Aptitude Questions and Answers
- Time and Distance Quiz
- Problems on Trains Quiz
- Time and Work Online Test
- Partnership Questions Answers
- Ratio and Proportion Quiz
- Boats and Streams Questions
- Simple Interest Online Test
- Areas Questions Answers
- Problems on LCM and HCF Quiz
- Pipes and Cisterns Questions
- Problems on Numbers Quiz
- Compound Interest Questions
- Volume & Surface Area Quiz
- Profit and Loss Online Test
- Odd Man Out Online Test
- Races and Games Quiz
- Numbers and Ages Quiz
- Mixtures and Alligations Quiz
- Percentages Questions Answers
- Simple Equations Quiz
- Quadratic Equations Quiz
- Surds and Indices
- Mensuration Questions Answers
- Permutations Online Test
- Probability Questions Answers
- Simplification Online Test